Ejercico

antecedentes de la geometria 1.2

 GEOMETRÍA ANALÍTICA



La geometría analítica es la rama de la geometría en la que las líneas rectas,
las curvas y las figuras geométricas se representan mediante expresiones
algebraicas y numéricas usando un conjunto de ejes y coordenadas. Cualquier
punto del plano se puede localizar con respecto a un par de ejes
perpendiculares dando las distancias del punto a cada uno de los ejes.
La geometría avanzó muy poco desde el final de la era griega hasta la edad
media. El siguiente paso importante en esta ciencia lo dio el filósofo y
matemático francés René Descartes, cuyo tratado El Discurso del Método,
publicado en 1637, hizo época. Este trabajo fraguó una conexión entre la
geometría y el álgebra al demostrar cómo aplicar los métodos de una disciplina
en la otra. Éste es un fundamento de la geometría analítica, en la que las
figuras se representan mediante expresiones algebraicas, sujeto subyacente en
la mayor parte de la geometría moderna

2.2 Sistemas de Coordenadas

Un sistema de coordenadas es un conjunto de valores y puntos que permiten
definir unívocamente la posición de cualquier punto de un espacio euclídeo o
más generalmente variedad diferenciable.

A continuación se han construido dos rectas reales perpendiculares entre sí en
las que el origen coincide. Esto constituye un Sistema de Coordenadas
Cartesianas ― o rectangulares ― en el plano y las rectas se llaman ejes. El eje
horizontal es el eje de las x y la recta vertical el eje de las y como se ha
señalado en el dibujo.

En este, debe ubicar un punto P en el plano. Constrúyase una recta
perpendicular al eje de las x a 130 pixeles desde el origen, al punto sobre el eje
x le llamara X. Construya también una perpendicular a 230 pixeles del origen
en el eje “y” y rotúlelo sobre el eje y como Y (230 pixeles = 2,30 unidades
gráfico).



Ubique en un plano cartesiano aproximadamente el punto X = -1,5 sobre el eje
x valor de la primera componente; y punto Y = 2 sobre el eje y o valor de la
segunda componente

2.2 Conceptos fundamentales

Sean A y B dos conjuntos de elementos. Si a cada elemento de A se le asocia
un elemento de B, entonces decimos que la asociación está definida por una
función f, de A a B y la escribiremos como f; A→B.

Por ejemplo, sea A = {1, 2, 3} y B = {a, b}. Definiremos f; A→B por el siguiente
diagrama:

 1 →a, 2 →b, 3 →a
 Con el elemento 1, f asocia a:____
 Con el elemento 2, f asocia a: ____
 Con el elemento 3, f asocia a: ____

Por lo tanto, es evidente qué la función asocia a cada elemento del conjunto B
un elemento del conjunto A
Una función puede definirse como un conjunto de pares ordenados (x, y) en
donde, x pertenece al dominio de la función e y = f(x) es la regla de
correspondencia que permite calcular la segunda componente y para cualquier
primer componente x.

2.3 Línea Recta

Una línea recta, lo mismo que cualquier curva está contenida totalmente en un
plano cartesiano, por una función de dos variables, siempre y cuando dicha
función sea capaz de expresar la condición común que satisfacen
absolutamente todos y cada uno de los puntos que constituyen dicha línea.

Por ejemplo, si pensamos en una línea recta paralela al eje de las abscisas,
necesitamos empezar por saber dónde está trazada dicha paralela, lo que en el
-3 -2 -1 O 1 2
3
1
2
3
-1
-2
-3
y
x caso de nuestra Figura 1 equivale a conocer la distancia b. Además, es muy
importante admitir que absolutamente todos los puntos de la paralela en
cuestión, cualquiera que sea la abscisa, tiene una ordenada constantemente
igual a b, razón por lo que la función representativa de esta paralela tiene que
ser y=b sin que tenga que intervenir la variable x porque para nada influye en el
valor de y. Si la constante b es positiva la paralela está situada arriba del eje de
las x y, si es negativa abajo.


La recta, o linea recta, en geometría, es el ente ideal que sólo posee una
dimensión, y contiene infinitos puntos; esta compuesta de infinitos segmentos
(el fragmento de línea más corto que une dos puntos); también se describe
como la sucesión continua e indefinida de puntos en una sola dimensión

ECUACIÓN DE LA RECTA

Tomados dos puntos de una recta, la pendiente , es siempre constante. Se
calcula mediante la ecuación:
Se puede obtener la ecuación de la recta a partir de la fórmula de la pendiente:

Esta forma de obtener la ecuación de una recta se suele utilizar cuando se
conocen su pendiente y las coordenadas de uno de sus puntos, o cuando se
conocen sólo los dos puntos, por lo que también se le llama ecuación de la
recta conocidos dos puntos, y se le debe a Jean Baptiste Biot. La pendiente m
es la tangente de la recta con el eje de abscisas.

Ecuación de la recta ordinaria Si se conoce la pendiente m, y el punto donde la recta corta al eje de
ordenadas es (0, b), podemos deducir, partiendo de la ecuación general de la
recta, y2 − y1 = m(x2 − x1):




Esta es la segunda forma de la ecuación de la recta y se utiliza cuando se
conoce la pendiente y la ordenada al origen, que llamaremos b. También se
puede utilizar esta ecuación para conocer la pendiente y la ordenada al origen
a partir de una ecuación dada.
La ecuación general de una recta es una expresión de la forma Ax+By+C=0, donde
A, B y C son números reales.
La pendiente de la recta es el coeficiente de la x una vez puesta en forma explícita
(es decir, despejada y):
By = -Ax-C -> -> la pendiente es: m = -A/

antecedentes de la geometria 1.1

ANTECEDENTES HISTÓRICOS DE LA GEOMETRÍA ANALÍTICA

 
 

Los antecedentes de la  geometría clásica se centraron en la orientación y en la correcta construcción de edificios. Ahora en los tiempos modernos, los conceptos geométricos se han generalizado con un alto nivel de abstracción y complejidad, y han sido sometidos a los métodos de cálculo y álgebra abstracta, de modo que muchas modernas ramas son apenas reconocibles como las descendientes de los principios de la geometría.

Los primeros grabados sobre la geometría se remontan a la época de los cavernícolas, cuando se  descubrió obtusos triángulos en el antiguo Valle del Indo (Harappan), y en la antigua Babilonia alrededor del 3000 AC.

 Los principios de la geometría eran una colección de principios empíricamente descubiertos en relación con las longitudes, ángulos, áreas, y volúmenes, y que fueron desarrollados para satisfacer algunas necesidades en la agrimensura, la construcción, la astronomía, y diversas artesanías. Entre estos principios, destacan algunos sorprendentemente sofisticados, que para la matemática moderna o para un matemático le pueden resultar difícil de obtener algunos de ellos sin el uso del cálculo moderno. Por ejemplo, tanto los egipcios como los babilonios eran conscientes de las versiones del teorema de Pitágoras aproximadamente 1500 años antes que Pitágoras; los egipcios tenían una fórmula correcta para el volumen de un tronco de una pirámide cuadrada; los babilonios disponían de tablas de trigonometría.

 

GEOMETRÍA EGIPCIA

Los antiguos egipcios conocían la forma de aproximarse al área de un círculo de la siguiente manera:

Área del círculo = [ (Diámetro) x 8/9 ]²

El problema nº 50 del papiro de Ahmes utiliza este método para obtener la superficie de un círculo de acuerdo con la norma de que el área es igual al cuadrado de 8 / 9 del diámetro del círculo. Esto supone que π es de 4 × (8 / 9) ² (3.160493 ...), con un error de poco más de 0,63 por ciento.

Este valor es ligeramente menos preciso que los cálculos de los babilonios (25 / 8 = 3,125, con un error del  0,53 por ciento), pero no fue superado hasta la llegada de Arquímedes cuya aproximación fue de 211875/67441 = 3,14163, donde había un error de poco más de 1 entre 10000 ).

En el problema 48 se usaba un cuadrado de lado de 9 unidades. Esta pieza fue cortada en forma de  cuadrícula de 3x3. Los cuadrados de las diagonales fueron utilizados para hacer un octógono irregular con una superficie de 63 unidades. Esto dio un segundo valor de π de 3,111 ... 

Los dos problemas juntos indicaron un rango de valores de Pi entre 3.11 y 3.16. 

El problema 14 del Papiro de Moscú muestra un único ejemplo antiguo al encontrar el volumen de un tronco de una pirámide, describiendo la fórmula correcta:

V = 1/3 * h(X1²  + X1*X2 + X2²)

GEOMETRÍA BABILONIA

Los babilonios  conocían las normas generales para la medición de áreas y volúmenes. Se medía la circunferencia de un círculo como tres veces el diámetro  lo que sería correcto si π fuese estimado como valor 3. El volumen de un cilindro se tomó como el producto de la base y la altura, sin embargo, el volumen del tronco de un cono o una pirámide cuadrada fue tomada incorrectamente como el producto de la altura y la mitad de la suma de las bases.

El teorema de Pitágoras era también conocido por los babilonios. Los babilonios también son conocidos por la milla babilónica, que fue una medida de distancia igual a siete millas actuales.

GEOMETRÍA INDIA

Periodo Harappan:

Las primeras pruebas y antecedentes de la utilización de las matemáticas en el sur de Asia se encuentra en los artefactos de la civilización del Valle Indus , también llamada Harappan , durante el 3er milenio aC. Las excavaciones en Harapa, Mohenjo-Daro (en la actual Pakistán), Lothal (en la actual India) y otros lugares a lo largo del valle del río Indus han descubierto pruebas de la utilización de las matemáticas. Estos pueblos fabricaban ladrillos cuyas dimensiones eran de la proporción 4:2:1, considerado favorable para la estabilidad de una estructura de ladrillo. Utilizaron un sistema normalizado de pesos sobre la base de los ratios: 1 / 20, 1 / 10, 1 / 5, 1 / 2, 1, 2, 5, 10, 20, 50, 100, 200, y 500, con la unidad peso que tiene aproximadamente 28 gramos.

Principios basicos

Presentacion

Euclides y axioma

EUCLIDES

Matemático griego. Poco se conoce a ciencia cierta de la biografía de Euclides, pese a ser el matemático más famoso de la Antigüedad. Es probable que se educara en Atenas, lo que permitiría explicar su buen conocimiento de la geometría elaborada en la escuela de Platón, aunque no parece que estuviera familiarizado con las obras de Aristóteles.

Euclides enseñó en Alejandría, donde alcanzó un gran prestigio en el ejercicio de su magisterio durante el reinado de Tolomeo I Zóster; se cuenta que éste lo requirió para que le mostrara un procedimiento abreviado para acceder al conocimiento de las matemáticas, a lo que Euclides repuso que no existía una vía regia para llegar a la geometría (el epigrama, sin embargo, se atribuye también a Maneco como réplica a una demanda similar por parte de Alejandro Magno).

AXIOMA

Un axioma es una proposición que se considera «evidente» y se acepta sin requerir demostración previa. En un sistema hipotético-deductivo es toda proposición no deducida (de otras), sino que constituye una regla general de pensamiento lógico (por oposición a los postulados).

En lógica y matemáticas, un axioma es una premisa que, por considerarse evidente, se acepta sin demostración, como punto de partida para demostrar otras fórmulas. Tradicionalmente los axiomas se eligen de las consideradas «afirmaciones evidentes», porque permiten deducir las demás fórmulas.

En lógica un postulado es una proposición no necesariamente evidente: una fórmula bien formada (planteada) de un lenguaje formal utilizada en una deducción para llegar a una conclusión.

En matemática se distinguen dos tipos de proposiciones: axiomas lógicos y postulados

EJERCICIOS

A) EN LA FIGURA "A" SI M<Y = 46° CALCULE M<X.
B)EN LA FIGURA "B"  SI M<Y= 112° CALCULE M<X
C)EN LA FIGURA "C" SI  M<X=75 CALCULE M<X.



resultado
x= 23°
y=46°

   

 

 

x=34°

y= 112°

 

  
x= 75°
y= 90°

TEOREMA DE PITAGORAS

 

 

Establece que en todo triangulo rectángulo el cuadrado de la hipotenusa es igual ala suma de los cuadrados de los catetos.

 

 

y en todo triangulo rectángulo el cuadrado de la hipotenusa es igual ala suma de los cuadrados de los catetos

 

si un triangulo rectángulo tiene  catetos de longitudes a y b y la medida de la hipotenusa es "c" se establece que c2 =  a2 + b2.

Teoremas

TEOREMA 1

Si cualquier recta paso por el centro del circulo y es perpendicular a una de las cuerdas entonces bisecta a dicha cuerda.

TEOREMA 2

Si cualquier circulo dos cualesquiera de sus cuerdas son congruentes entonces dichas cuerdas  equidistan de su centro .

TEOREMA 3

Dos o mas círculos son congruentes si tienen sus radios respectivamente congruentes .

TEOREMA 4

Si una recta es tangente de un circulo entonces el radio trazado al punto de tangencia es perpendicular ala tangente.

TEOREMA 5

Si desde un punto exterior a un mismo circulo se trazan tangentes a  el, entonces
a) los segmentos tangentes determinados porel punto exterior y los puntos de tangencia son congruentes.

Circulo y Poligonos

Circulo:

Es un conjuntos de los puntos en un plano que están a la misma distancia de un punto fijo llamado centro.

 

Circunferencia:

 

La circunferencia de un circulo es la distancia al rededor de un circulo y tiene 360°

 

Radio:

 

El radio es justo la mitad del diámetro. Todos los radios de una figura geométrica poseen la misma longitud.

 

 

 

 

 

 

polígonos:

 

un polígono inscrito es un polígono tal que sus lados son cuerdas de un circulo.

 

un polígono circunscrito es un polígono tal que todos los lados son tangentes tal que todos sus lados son tangentes a un circulo.

Un circulo circunscrito es el que pasa por todos los vértices de un polígono.

 

 

Un circulo inscrito es aquel para el que son tangentes los lados de un polígono.

 

 

 

 

 

 

Geometria y Trigronometria: Circulos

Geometria y Trigronometria: Circulos: un circulo es el conjunto en que todos los puntos de un plano son equidistantes de un punto fijo denominado centro  la circunferencia de un ...

poligonos, trapezoides y paralelogramos

Polígonos y sus medidas

* un polígono es una figura plana cerrada acotado por segmento de línea recta como lados.
* un n-gono en un polígono de n lados.
* un polígono regular; es equilátero y equiángulo.

Suma de las medidas de los ángulos internos de interno de polígono.

*al trazar diagonales desde un vértice hasta cada unos de los otros es posible dividir un polígono de siete lados en cinco triángulos

* nótese que cada triangulo le pertenece uno de los lados del polígono exepto por el primero y el ultimo triangulo los cuales tienen a dos de ellos.

Entonces

* con este proceso se divide un polígono de n lados en n-2 triángulos
* la suma de las medidas de los ángulos internos de un polígono es iguala las medidas de los angulos  interno de los triángulos

                                        TRAPEZOIDE

*un trapezoide es un cuadrilátero que tiene dos lados paralelos

*las bases del trapezoide son sus lados paralelos

*los lados son sus partes no paralelas

*la medida de un trapezoide es un segmento que une a los puntos medios  de sus lados

*un trapezoide isósceles tiene sus lados congruentes

 

                                                 PARALELOGRAMOS

Un paralelogramos es un cuadrilátero cuyos lados son paralelos.

la diagonal de un paralelogramo lo divide en triángulos congruentes

los ángulos consecutivos de un paralelogramo son suplementarios

las diagonales de un paralelogramo se bisecta entre si.

Principios basicos de los triangulos

si dos ángulos son congruentes sus lados o ángulos correspondientes son congruentes

1_ si dos triángulos son congruentes entonces sus partes correspondientes son congruentes
2_ si dos lados y el ángulo comprendido de un ángulo son congruentes con las partes correspondientes de otro entonces los triángulos son congruentes.

Ejercicios












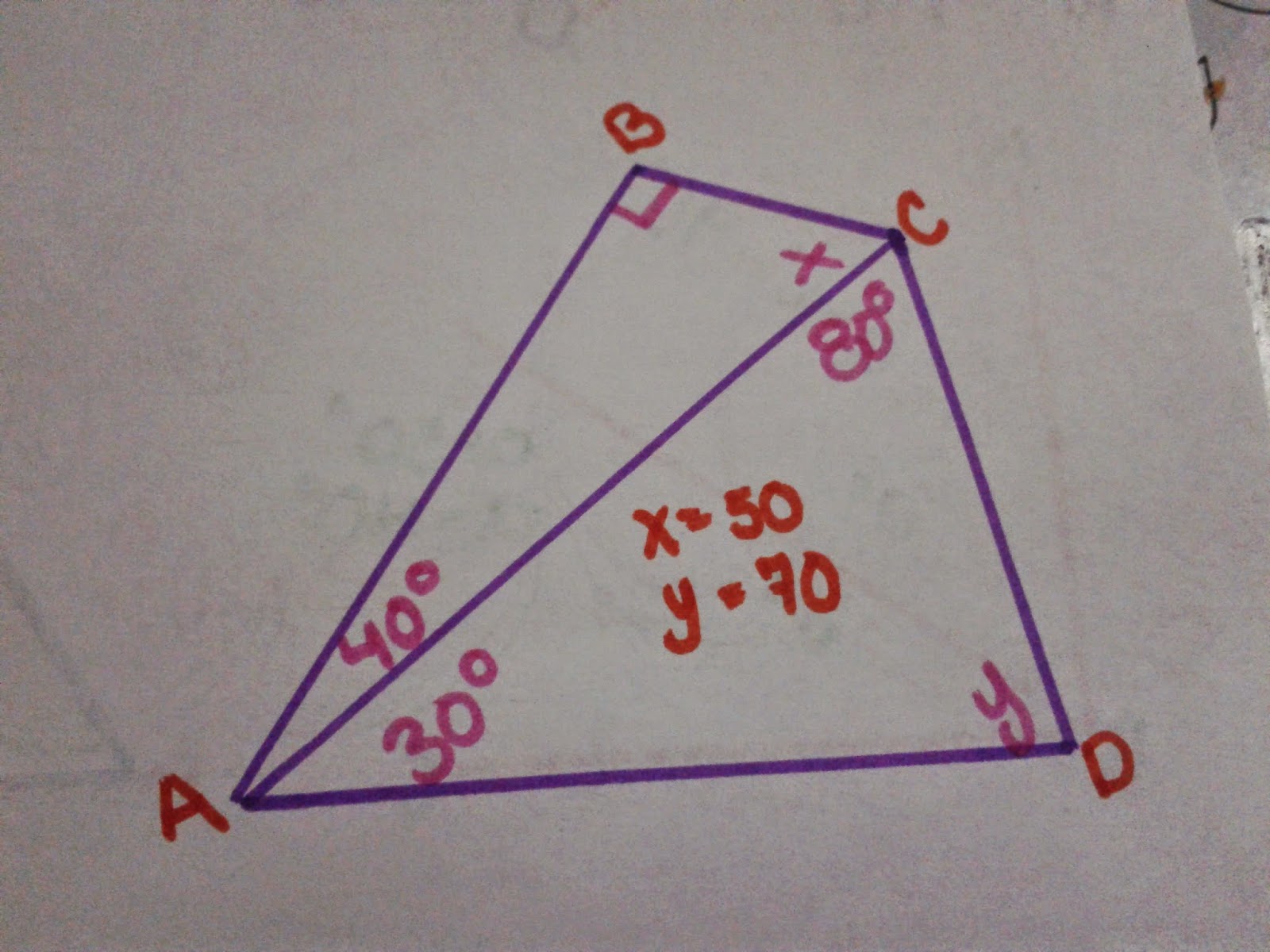
si dos  lados ángulos  son respectivamente parales entre si entonces ya sea que los ángulos son congruentes o son suplementarios...

Encuentra la medida de "x" y la medida "y" de los ángulos indicados

Ejercicios

Hallar los valores de " X y Y "

 

 

 

 

Mediana, Mediatriz, bisectriz y Altura

 

La mediatriz de un segmento es la recta que pasa por el punto medio del segmento y es perpendicular al él.

 

Mediana : segmento de recta trazada desde cualquiera de los vértice y cae en el punto medio del lado opuesto

 

La bisectriz de un ángulo es la recta que pasando por el vértice del ángulo lo divide en dos ángulos iguales.

 

Es una línea que se traza perpendicularmente des de un vértice hasta la mitad de un segmento opuesto

 

 

 

Tipos de pares de angulos

Ángulos adyacentes son dos ángulos que tienen el mismo vértice y un lado en común

 

 

Ángulos compuestos por el vértice son dos ángulos no adyacentes formados por dos líneas que se intersectan.

Los ángulos opuestos por el vértice son congruentes

Ángulos complementarios son dos ángulos que suman en total 90°.















Ángulos suplementarios  son dos ángulos que suman 180°

 

Triangulos

Un triángulos puedes designarse por medio de tres letras mayúsculas en cualquier orden y por medio de un numero romano dentro del símbolo

Clasificación de triángulos dependiendo de los ángulos

Agudo
Recto
Obtuso


Líneas especiales en un triangulo

Angulos

Un ángulo es la figura formada por dos rayos con un punto en común.

Los rayos son los lados del ángulo y punto terminal es su vértice.

Medición de ángulos

El tamaño de un ángulo después de que tanto debe rotarse unos de sus lados hasta que coincida con el otro lado. El tamaño de un ángulo no depende de la longitud de los lados del ángulo.

Tipos de ángulos














Perpendiculares son líneas rayos o segmentos que se intersectan formando ángulos rectos  .

Circulos

un circulo es el conjunto en que todos los puntos de un plano son equidistantes de un punto fijo denominado centro  la circunferencia de un circulo es la distancia al rededor del circulo es decir su perímetro contiene 360°.

Radio es segmento en que une dos puntos cualesquiera de un circulo.

Un diámetro es una cuerda que pasa por el centro de un circulo es la cuerda mas grande y tiene el doble de longitud del radio .

Un arco es una parte continua de un circulo.

Un semicírculo es un arco que mide la mitad del circunferencia de un circulo.
los círculos congruentes son círculos con radios congruentes

Segmentos congruentes

Dos segmentos son congruentes solamente si tienen exactamente la misma longitud.

Dos segmentos son congruentes cuando superpuestos coinciden en todos sus puntos. Para ello basta con mostrar que

coinciden en sus extremos.

Es decir que si por algún tipo de desplazamiento o movimiento pudiésemos poner un segmento sobre otro, todos sus puntos coincidirían.

Los segmentos a y b son congruentes, si desplazamos el segmento b sobre el a y hacemos coincidir el punto C con el punto A, también podemos hacer coincidir los puntos B y D.

 Cuando dos segmentos son congruentes se dicen que tienen la misma longitud.

 

Segmentos de linea

un segmento de linea es la parte entre dos puntos en una línea recta, incluyendo estos dos puntos. Se designa por las letras mayúsculas que representan a estos puntos o por una letras mayúsculas que representan a estos puntos o por una letra minúscula

A_____r_____B

División de un segmento de líneas en partes

si dividimos un segmento de líneas es partes :
1_ la longitud del segmento completo es igual a la suma de las longitudes de sus partes ; A____B____C____D = AB+ BC+CD= AD

2. la longitud del segmento de línea completo es mayor que la longitud de cualquiera de sus partes si un segmento de línea se divide en dos partes iguales. 1. el punto de división es el punto medio del segmento de la línea . 2. se dice que una línea bisecta el segmento cuando pasa por el punto medio de un segmento.

 

 

3.si tres puntos " a,b, y c " están sobre una línea decimos que son colineales si a, b y c son colineales y a.b mas b,c es igual ac entonces b esta entre a y c A_____B_____C  AB+BC=AC

 

 

Punto,Linea y Plano

un punto solo tiene posesión. no tiene longitud anchura o grosor. (  ^. M   )

 

una línea o recta tiene longitud pero no anchura o grosor, una línea puede ser recta  o curva o una combinación de ambas, y una línea puede extenderse en forma limitada en cualquier dirección infinitivamente.

 

un rayo es la parte de una línea recta que comienza en un punto dado y que se extiende en forma ilimitada en una dirección .

 

un plano tiene longitud y anchura pero no espesor, puede representarse por un pizarrón

 o el lado de una caja una superficie plana es una superficie tal que si una línea recta conecta dos puntos cualesquiera esta queda contenida en forma total.

 

 

Ejemplo

a_ cubierta de un escritorio............................. plano

b_ una pantalla cinematográfica............................... plano

 c_ el filo de una regla.............................................línea

d_ un hilo en tensión.......................................línea

e_ la punta de un alfiler......................................punto



Antensedentes de la Geometria

la palabra geometría se deriva de los vocablos geos, tierra y metrón mediana. los antiguos egipcios, chinos babilonios romanos y griegos utilizan la geometría en la navegación, astronomía y otras labores practicas. Con frecuencia se busca la relación que existe entre dos o mas figuras geométricas. En todas las épocas el hombre a utilizado las sencillas formas geométricas que sugiere la naturaleza para la creación de objetos útiles e interesantes. debido a que estamos rodeados de objetos es comprensible la importancia que tiene el poder hablar sobre ellos. Al comunicarnos con otras personas para describir el modo en que vivimos necesitamos un lenguaje de geometría.